Module de Formation PE "Astronomie" - Documentation scientifique

Le système solaire : le modèle de Kepler (héliocentrique)

Les faiblesses du modèle copernicien (héliocentrique).

L' apport essentiel du système de Copernic est d'être un modèle simple : les planètes tournent autour du Soleil sur des trajectoires circulaires avec une vitesse constante. Ce modèle est compatible avec le mouvement rétrograde des planètes observé par rapport à la sphère des étoiles. Cependant,  il restait  un  bon  nombre de  discordance  entre  les  observations et les prévisions du modèle copernicien.  A titre d'exemple :

• les observations montrent que les planètes ne se déplacent pas de manière uniforme et que la distante au Soleil ne reste pas constante. 

Le modèle de Kepler

Kepler s'appuie sur les observations très minutieuses de Tycho Brahé qui établit des tables très précises des positions des planètes.  Il compare les calculs des orbites de Mars et de la Terre dans les différents systèmes (Copernic, Ptolémée, ...).

Il propose un nouveau modèle basée sur 3 lois  :
 

1) Chaque planète décrit une ellipse dont un des foyers est occupé par le Soleil.

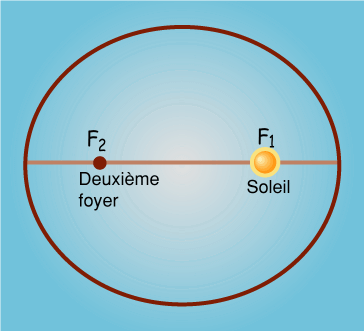
Que cela signifie-t-il exactement au niveau de la description des trajectoires des planètes du Système Solaire?
On peut caractériser une ellipse par son excentricité e (cliquer ici pour apprendre à tracer une ellipse connaissant e).
Dans le système solaire,  les excentricité  prennent des valeurs entre 0 et 0,25.

La figure 1 ci-dessous montre deux trajectoires :
1) Celle de Vénus dont l'excentricité vaut 0 : la trajectoire est un cercle et le Soleil est placé au centre du cercle.
2) Celle de Mercure dont l'excentricité vaut 0.2 :  le Soleil est placé sur le foyer de l'ellipse (ce qui revient ici à décaler la trajectoire),  la courbe est quasiment un cercle.

2) La droite joignant la planète au Soleil balaie des aires égales en des temps égaux.

Kepler introduit ici le fait que les planètes ont une vitesse plus élevées lorsqu'elles sont proches du Soleil et plus faibles lorsqu'elles en sont éloignées.

3) Le carré du temps de révolution d’une planète autour de son orbite est proportionnel au cube de la distance moyenne au Soleil. Symboliquement, cette loi s’écrit :

 T2 = k r3

La constante k étant la même pour toutes les planètes.

 

Cette loi indique que plus on s'éloigne plus on met de temps pour faire un tour. Autrement dit,  la période de  révolution  de la  planète autour du Soleil croît (non linéairement)  en fonction de la distance par rapport au Soleil.