Les transformations de mouvements
R <=> R

Les solutions de transformations de mouvements vues jusqu'à présent (engrenages, poulies / courroie, pignons / chaîne) sont des solutions où les axes
de rotation sont parallèles.

Pour transmettre un mouvement de rotation lorsque les axes sont perpendiculaires, deux dispositions constructives sont couramment utilisées :

Les pignons coniques



Les résultats obtenus avec les pignons cylindriques sont identiques :

relation entre diamètre de fonctionnement et nombre de dents
 calcul du rapport de réduction
On trouve ce type de pignons par exemple dans les différentiels de voiture, dans les renvois d'angles ... mais aussi sur une chignole (image
ci-dessous)  et d'une manière très proche sur le batteur mécanique ci-desous.

 


Le système roue et vis sans fin
Ce système, lui aussi très répandu, ce compose d'une roue dentée (les dents ne sont pas droites) et d'une vis. Les dents de ces deux pièces sont "complémentaires" si bien que la transmission du mouvement peut se faire.

Pour monrer la transformation du mouvement, on considère le bâti suivant :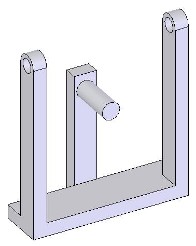



Dans ce bâti, viennent pivoter la roue (rouge) et la vis (bleue). Cette dernière est munie d'un "bras" pour mieux visualiser son mouvement. Voir images ci-dessous :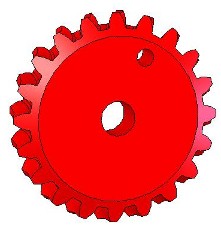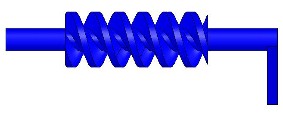

   

Cliquer sur l'image ci-dessous pour voir l'animation de cette transformation de mouvement.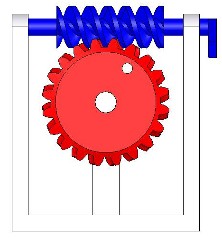




Suite : R <=> T