
|
|||||||||||||||
On définit le rapport de réduction d'un
engrenage comme étant le rapport entre le nombre de tours du
pignon de sortie sur le nombre de tours du
pignon d'entrée. Pendant le même intervalle de temps, ce rapport est aussi égal à la vitesse de rotation du pignon de sortie (notée Ns) sur celle du pignon d'entrée (Ne). On note k ce rapport.
Considérons un mécanisme comportant deux pignons engrenant l'un sur
l'autre.
Ce mécanisme comporte un bâti (fixe), représenté sur l'image gauche ci-dessous. Une perspective de l'ensemble permet de mieux situer la position des différentes pièces. 
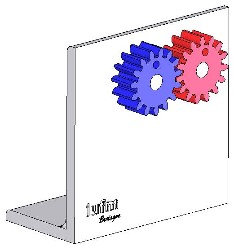 De cet exemple on a choisi Ze = Zs. Le pignon bleu est le pignon "moteur", le pignon d'entrée. Des trous ont été effectués sur les pignons pour mieux visualiser leur mouvement. Pour visualiser une courte séquence vidéo, cliquer sur l'image.  On tire deux conclusions : On en déduit que pour ce cas :
On choisit désormais Zs = 2 Ze (gauche) ou Zs = 4 Ze (droite). Cliquer sur les images voir voir les séquences vidéo. 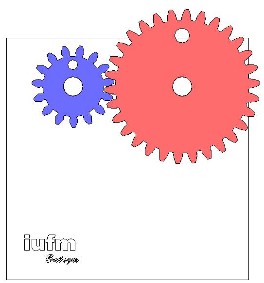
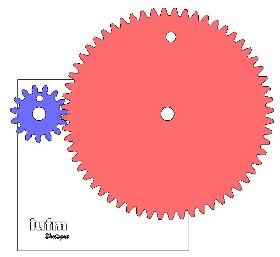 Le pignon bleu étant toujours en entrée, on observe que :
Le rapport de réduction est toujours négatif car les deux pignons tournent en sens contraire. Il est inversement proportionnel au rapport des nombres de dents. Considérons deux mécanismes à trois pignons dans lesquels on a Ze = Zs. Cliquer sur les images voir voir les séquences vidéo. 
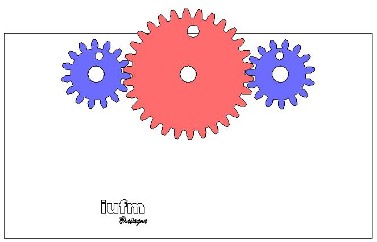 Dans ce cas, les roues d'entrée (celle de gauche) et de sortie (celle de droite) tournent dans le même sens. Les dimensions du pignon intermédiaire n'interviennent pas. On a alors :
On peut généraliser les observations précédentes avec cet autre exemple, où le pignon d'entrée (bleu) à un diamètre 4 fois plus petit que le pignon de sortie (rouge). Cliquer sur l'image voir voir la séquence vidéo. 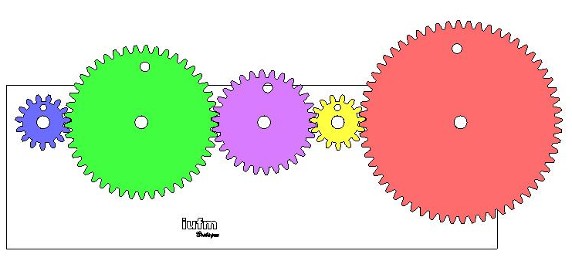 L'observation de cette séquence vidéo nous permet de proposer la formule ci-dessous :
Attention, la précédente relation n'est valable que si les contacts sont extérieurs. Dans le cas d'un contact intérieur (un pignon roule sans glisser sur une couronne dentée), le sens de rotation est inversé. Dans l'exemple suivant, la roue de sortie (rouge) a 3 fois plus de dents que le pignon d'entrée (bleu). Cliquer sur l'image voir voir la séquence vidéo. 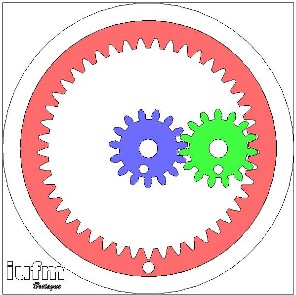 La "formule" qui généralise toutes les observations précédentes est donc :
Pour la suite (transmission par poulies / courroie), cliquez ici.
|