Les courroies sont des liens flexibles qui permettent de transmettre le mouvement par des poulies.
Ces courroies peuvent être crantées ou lisses.

On trouve par exemple des courroies dans un lecteur de disquettes ; voir image ci-dessous :



On en recontre également dans des machines agricoles, des machines à coudre, dans un alternateur de voiture ...

Avantage par rapport à la solution "engrenage" : possibilité d'avoir des entraxes très importants entre les deux axes de rotation.


Premier exemple

Considérons deux poulies de même diamètre ; l'une est bleue, l'autre rouge dans l'image ci-dessous. La courroie est verte.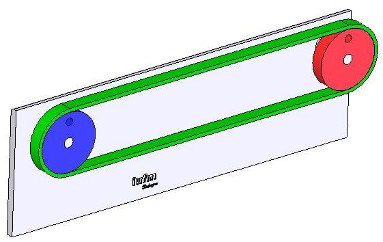



Cliquer sur l'image ci-dessous pour avoir accès à une séquence vidéo.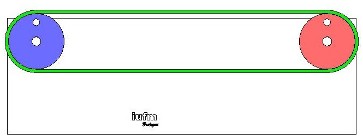


Conclusions :
Les deux poulies tournent dans le même sens (k > 0). Elles tournent à la même vitesse.
Donc :

k = 1

Deuxième exemple

On considère une poulie motrice (en entrée du mécanisme) de diamètre De.
La poulie en sortie a un diamètre Ds = De / 2.

Cliquer sur l'image ci-dessous pour avoir accès à une séquence vidéo.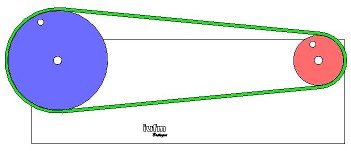



Conclusion :

k = De / Ds

Cette dernière relation est toujours valable dans le cas d'une liaison pignons / chaîne que l'on trouve par exemple sur les vélos :



Une courroie pouvant glisser sur les poulies, on devine que la solution pignons / chaîne permet de transmettre des efforts plus importants.

Un pignon possède des obstacles, comme une roue dentée ; ces obstacles ont une géométrie telle qu'ils permettent à la chaîne de transmettre le
mouvement (cf. images ci-dessous).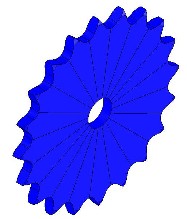

     

Ce type de pignon ne peut pas être utilisé dans un engrenage ; la géométrie des dents ne permet ni transmettre le mouvement, ni de transmettre les efforts.

En guise d'exercice, on pourra vérifier qu'un plateau (grand pignon lié au pédalier) de 52 dents et un pignon de 14 dents (lié à la roue arrière motrice de diamètre 680 mm) permet au cycliste d'atteindre une vitesse d'environ 38 km/h lorsqu'il pédale à 80 tours/minute.


Pour la suite, cliquez ici.